How To Determine If A Precipitate Will Form From Ksp

16.3: Precipitation and the Solubility Product

1. Last updated

2. Relieve as PDF

Page ID

41632

Learning Objectives

• Define Yard _sp, the solubility product.
• Explain solid/solution equilibria using \(K_{sp}\) and Q _sp.
• Calculate molarity of saturated solution from Thou _sp.
• Calculate \(K_{sp}\) from molarity of saturated solution.

Precipitation reactions occur when cations and anions in aqueous solution combine to form an insoluble ionic solid called a precipitate. Whether or not such a reaction occurs tin be determined by using the solubility rules for mutual ionic solids. Because not all aqueous reactions form precipitates, ane must consult the solubility rules before determining the state of the products and writing a cyberspace ionic equation. The power to predict these reactions allows scientists to determine which ions are nowadays in a solution, and allows industries to form chemicals by extracting components from these reactions.

Properties of Precipitates

Precipitates are insoluble ionic solid products of a reaction, formed when certain cations and anions combine in an aqueous solution. The determining factors of the formation of a precipitate tin vary. Some reactions depend on temperature, such every bit solutions used for buffers, whereas others are dependent but on solution concentration. The solids produced in precipitate reactions are crystalline solids, and can be suspended throughout the liquid or autumn to the bottom of the solution. The remaining fluid is called supernatant liquid (or just the supernate). The ii components of the mixture (precipitate and supernate) can be separated by various methods, such equally filtration, centrifuging, or decanting.

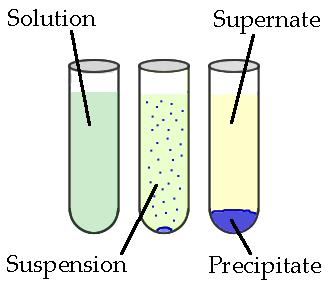
Figure \(\PageIndex{1}\): Above is a diagram of the germination of a precipitate in solution. (Public Domain; ZabMilenko)

The utilise of solubility rules require an understanding of the way that ions react. Well-nigh atmospheric precipitation reactions are single replacement reactions or double replacement reactions. A double replacement reaction occurs when two ionic reactants dissociate and bond with the respective anion or cation from the other reactant. The ions replace each other based on their charges as either a cation or an anion. This tin exist thought of as a double deportation reaction where the partners "switching; that is, the two reactants each "lose" their partner and form a bond with a different partner:

Figure \(\PageIndex{ii}\): A double replacement reaction

A double replacement reaction is specifically classified as a atmospheric precipitation reaction when the chemical equation in question occurs in aqueous solution and one of the of the products formed is insoluble. An example of a atmospheric precipitation reaction is given below:

\[\ce{CdSO4(aq) + K2S (aq) \rightarrow CdS (s) + K2SO4(aq)}\]

Both reactants are aqueous and one production is solid. Considering the reactants are ionic and aqueous, they dissociate and are therefore soluble. Still, at that place are half-dozen solubility guidelines used to predict which molecules are insoluble in water. These molecules form a solid precipitate in solution.

Solubility Rules

Whether or not a reaction forms a precipitate is dictated past the solubility rules. These rules provide guidelines that tell which ions class solids and which remain in their ionic grade in aqueous solution. The rules are to be followed from the top downwards, meaning that if something is insoluble (or soluble) due to rule 1, it has precedence over a college-numbered rule.

1. Salts formed with group 1 cations and \(\ce{NH_4^{+}}\) cations are soluble. There are some exceptions for certain \(Li^+\) salts.
2. Acetates (\(\ce{C2H3O2^{-}}\)), nitrates (\(\ce{NO3^{-}}\)), and perchlorates (\(\ce{ClO4^{-}}\)) are soluble.
3. Bromides, chlorides, and iodides are soluble.
4. Sulfates (\(\ce{SO4^{two-}}\)) are soluble with the exception of sulfates formed with \(\ce{Ca^{2+}}\), \(\ce{Sr^{ii+}}\), and \(\ce{Ba^{two+}}\).
5. Salts containing silver, lead, and mercury (I) are insoluble.
6. Carbonates (\(\ce{CO3^{ii-}}\)), phosphates (\(\ce{PO4^{three-}}\)), sulfides, oxides, and hydroxides (\(\ce{OH^{-}}\)) are insoluble. Sulfides formed with group two cations and hydroxides formed with calcium, strontium, and barium are exceptions.

If the rules land that an ion is soluble, and so it remains in its aqueous ion form. If an ion is insoluble based on the solubility rules, then it forms a solid with an ion from the other reactant. If all the ions in a reaction are shown to be soluble, then no precipitation reaction occurs.

Internet Ionic Equations

To understand the definition of a net ionic equation, recall the equation for the double replacement reaction. Because this item reaction is a atmospheric precipitation reaction, states of matter can be assigned to each variable pair:

\[\color{blueish}{A}\colour{red}{B}\color{black} (aq) + \color{blue}{C}\color{red}{D}\colour{blackness} (aq) → \colour{blue}{A}\color{reddish}{D}\colour{black} (aq) \colour{black}+ \color{blueish}{C}\color{red}{B}\color{blackness} (due south) \]

The first step to writing a net ionic equation is to separate the soluble (aqueous) reactants and products into their corresponding cations and anions. Precipitates practise not dissociate in h2o, so the solid should not be separated. The resulting equation looks like that below:

\[\colour{blue}{A}^+ \color{blackness} (aq) + \color{cherry-red}{B}\color{black}^- (aq) + \color{blueish}{C}\color{black}^+ (aq) + \color{cherry}{D}^-\colour{blackness} (aq) → \color{bluish}{A}^+\color{blackness} (aq) + \color{red}{D}^-\color{black} (aq) + \color{blue}{C}\color{red}{B}\color{blackness} (s) \]

In the equation above, A⁺ and D ^- ions are present on both sides of the equation. These are called spectator ions considering they remain unchanged throughout the reaction. Since they go through the equation unchanged, they can exist eliminated to show the net ionic equation:

\[ \color{cherry}{B}\colour{black}^- (aq) + \color{bluish}{C}\color{blackness}^+ (aq) → + \color{blue}{C}\color{cherry}{B}\color{blackness} (s) \]

The net ionic equation only shows the precipitation reaction. A net ionic equation must exist balanced on both sides non only in terms of atoms of elements, but also in terms of electric charge. Precipitation reactions are ordinarily represented solely by net ionic equations. If all products are aqueous, a internet ionic equation cannot be written because all ions are canceled out as spectator ions. Therefore, no precipitation reaction occurs

Equilibrium and non-Equilibrium Conditions

The ion product (Q) of a common salt is the product of the concentrations of the ions in solution raised to the same powers as in the solubility production expression. It is analogous to the reaction quotient (Q) discussed for gaseous equilibria. Whereas K _sp describes equilibrium concentrations, the ion production describes concentrations that are non necessarily equilibrium concentrations. An ion production tin can in principle take whatsoever positive value, depending on the concentrations of the ions involved. Only in the special case when its value is identical with Yard_{due south} does information technology become the solubility production. A solution in which this is the case is said to exist saturated. Thus when

\[[\ce{Ag^{+}}]^2 [\ce{CrO4^{ii-}}] = two.76 \times 10^{-12}\]

at the temperature and pressure at which this value \(K_{sp}\) of applies, we say that the "solution is saturated in silver chromate".

The ion product \(Q\) is coordinating to the reaction caliber \(Q\) for gaseous equilibria.

As summarized in Figure \(\PageIndex{3}\), in that location are three possible atmospheric condition for an aqueous solution of an ionic solid:

• \(Q < K_{sp}\). The solution is unsaturated, and more of the ionic solid, if available, volition deliquesce.
• \(Q = K_{sp}\). The solution is saturated and at equilibrium.
• \(Q > K_{sp}\). The solution is supersaturated, and ionic solid will precipitate.

Figure \(\PageIndex{3}\): The Relationship between Q and K_sp. If Q is less than 1000_sp, the solution is unsaturated and more than solid will dissolve until the system reaches equilibrium (Q = G_sp). If Q is greater than 1000_sp, the solution is supersaturated and solid will precipitate until Q = Yard_sp. If Q = K_sp, the rate of dissolution is equal to the rate of atmospheric precipitation; the solution is saturated, and no internet alter in the amount of dissolved solid will occur. (CC Past-SA-NC; Anonymous)

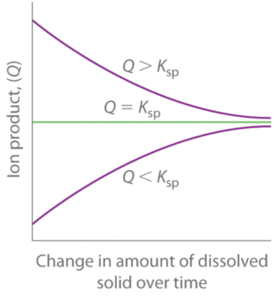
The procedure of calculating the value of the ion product and comparing it with the magnitude of the solubility product is a straightforward fashion to determine whether a solution is unsaturated, saturated, or supersaturated. More than important, the ion product tells chemists whether a precipitate will form when solutions of two soluble salts are mixed.

Example \(\PageIndex{3}\): barium milkshakes

Barium sulfate is used in medical imaging of the gastrointestinal tract. Its solubility product is \(1.08 \times 10^{−x}\) at 25°C, so it is ideally suited for this purpose because of its low solubility when a "barium milkshake" is consumed past a patient. The pathway of the sparingly soluble salt can be easily monitored by ten-rays. Volition barium sulfate precipitate if 10.0 mL of 0.0020 1000 Na₂And then₄ is added to 100 mL of 3.two × 10⁻⁴ M BaCl₂? Recall that \(\ce{NaCl}\) is highly soluble in water.

Given: One thousand _sp and volumes and concentrations of reactants

Asked for: whether precipitate will form

Strategy:

1. Write the balanced equilibrium equation for the atmospheric precipitation reaction and the expression for Grand _sp.
2. Determine the concentrations of all ions in solution when the solutions are mixed and use them to calculate the ion production (Q).
3. Compare the values of Q and Thou _sp to decide whether a precipitate will form.

Solution

A The only slightly soluble salt that can be formed when these two solutions are mixed is \(\ce{BaSO4}\) considering \(\ce{NaCl}\) is highly soluble. The equation for the precipitation of \(\ce{BaSO4}\) is equally follows:

\[\ce{BaSO4(s) <=> Ba^{ii+} (aq) + SO^{2−}4(aq)} \nonumber\]

The solubility product expression is as follows:

\[K_{sp} = [\ce{Ba^{ii+}}][\ce{SO4^{2−}}] = 1.08 \times 10^{−10} \nonumber\]

B To solve this problem, we must first calculate the ion product:

\[Q = [\ce{Ba^{ii+}}][\ce{SO4^{2−}}] \nonumber\]

using the concentrations of the ions that are present after the solutions are mixed and before any reaction occurs. The concentration of Ba^{2 +} when the solutions are mixed is the total number of moles of Ba^{2 +} in the original 100 mL of \(\ce{BaCl2}\) solution divided by the final book (100 mL + 10.0 mL = 110 mL):

\[ \begin{marshal*} \textrm{moles Ba}^{ii+}=\textrm{100 mL}\left(\dfrac{\textrm{1 50}}{\textrm{chiliad mL}}\right)\left(\dfrac{3.2\times10^{-4}\textrm{ mol}}{\textrm{1 50}} \correct )=3.2\times10^{-v}\textrm{ mol Ba}^{2+} \\[4pt] [\mathrm{Ba^{2+}}]=\left(\dfrac{3.2\times10^{-5}\textrm{ mol Ba}^{2+}}{\textrm{110 mL}}\right)\left(\dfrac{\textrm{grand mL}}{\textrm{1 50}}\correct)=2.9\times10^{-four}\textrm{ M Ba}^{2+} \end{align*}\]

Similarly, the concentration of SO_four ²⁻ later on mixing is the total number of moles of SO₄ ²⁻ in the original 10.0 mL of Na₂And so_iv solution divided past the final volume (110 mL):

\[ \begin{marshal*} \textrm{moles So}_4^{two-} &=\textrm{10.0 mL}\left(\dfrac{\textrm{one 50}}{\textrm{1000 mL}}\right)\left(\dfrac{\textrm{0.0020 mol}}{\textrm{ane L}}\correct)=2.0\times10^{-5}\textrm{ mol SO}_4^{2-} \\[4pt] [\mathrm{SO_4^{2-}}] &=\left(\dfrac{2.0\times10^{-five}\textrm{ mol So}_4^{2-}}{\textrm{110 mL}} \right )\left(\dfrac{\textrm{1000 mL}}{\textrm{i Fifty}}\right)=ane.viii\times10^{-4}\textrm{ Chiliad SO}_4^{two-} \end{align*}\]

We tin now calculate \(Q\):

\[Q = [\ce{Ba^{ii+}}][\ce{SO4^{2−}}] = (2.9 \times x^{−4})(1.8 \times ten^{−iv}) = five.2 \times 10^{−8} \nonumber \]

C We now compare \(Q\) with the \(K_{sp}\). If Q > Grand _sp, then \(\ce{BaSO4}\) will precipitate, only if Q < K _sp, it will not. Considering Q > One thousand _sp, nosotros predict that \(\ce{BaSO4}\) will precipitate when the two solutions are mixed. In fact, \(\ce{BaSO4}\) will continue to precipitate until the system reaches equilibrium, which occurs when

\[[\ce{Ba^{2+}}][\ce{SO4^{2−}}] = K_{sp} = 1.08 \times 10^{−10}. \nonumber\]

Exercise \(\PageIndex{3}\)

The solubility product of calcium fluoride (\(\ce{CaF2}\)) is \(three.45 \times 10^{−11}\). If 2.0 mL of a 0.10 1000 solution of \(\ce{NaF}\) is added to 128 mL of a \(2.0 \times ten^{−5}\,M\) solution of \(\ce{Ca(NO3)ii}\), will \(\ce{CaF2}\) precipitate?

Answer

Aye, since \(Q_{sp} = 4.vii \times x^{−11} > K_{sp}\).

A solution must be saturated to exist in equilibrium with the solid. This is a necessary status for solubility equilibrium, but it is not by itself sufficient. True chemical equilibrium can only occur when all components are simultaneously present. A solubility system tin can be in equilibrium only when some of the solid is in contact with a saturated solution of its ions. Failure to appreciate this is a very common cause of errors in solving solubility problems.

Undersaturated and supersaturated solutions

If the ion production is smaller than the solubility product, the system is not in equilibrium and no solid can be nowadays. Such a solution is said to exist undersaturated . A supersaturated solution is i in which the ion product exceeds the solubility product. A supersaturated solution is not at equilibrium, and no solid can ordinarily be nowadays in such a solution. If some of the solid is added, the backlog ions precipitate out and until solubility equilibrium is achieved.

How to know the saturation status of a solution? Just comparing the ion product Q_s with the solubility product M_{south p}. as shown in Tabular array \(\PageIndex{1}\).

Table \(\PageIndex{one}\): relationship amid \(Q_{sp}\), \(K_{sp}\) and saturation

\(Q_{sp}/K_{sp}\)	Condition
> 1	Product concentration as well high for equilibrium; net reaction proceeds to left.
= 1	System is at equilibrium; no net alter volition occur.
< one	Production concentration likewise depression for equilibrium; cyberspace reaction gain to right.

For instance, for the system

\[\ce{Ag2CrO4(due south) <=> ii Ag^{+} + CrO_4^{2–}} \label{4ba}\]

a solution in which Q_{due south}  < G_s (i.e., Thousand_s  /Q_s > 1) is undersaturated (blueish shading) and the no solid will exist present. The combinations of [Ag⁺] and [CrO_iv ^2–] that correspond to a saturated solution (and thus to equilibrium) are limited to those described past the curved line. The pinkish area to the right of this curve represents a supersaturated solution.

Effigy \(\PageIndex{4}\): Equilibrium vs. non-equilibrium states for \(\ce{Ag2CrO4(s)}\). (CC By; Stephen Lower).

For some substances, formation of a solid or crystallization does not occur automatically whenever a solution is saturated. These substances have a tendency to form oversaturated solutions. For example, syrup and honey are oversaturated saccharide solutions, containing other substances such as citric acids. For oversatureated solutions, Q _sp is greater than K _sp. When a seed crystal is provided or formed, a precipitate will class immediately due to equilibrium of requiring \(Q_{sp}\) to arroyo \(K_{sp}\). For case Sodium acetate trihydrate, \(\ce{NaCH3COO\cdot 3H2O}\), when heated to 370 Yard volition become a liquid and stays as a liquid when cooled to room temperature or even below 273 K (Video \(\PageIndex{1}\)). As soon as a seed crystal is present, crystallization occurs rapidly. In such a procedure, estrus is released since this is an exothermic process \(\Delta H < 0\).

Video \(\PageIndex{1}\): "hot ice" (sodium acetate) crystallized from a non-equilibrium supersaturated (\(Q_{sp} > K_{sp}\)) solution

Example \(\PageIndex{ane}\)

A sample of groundwater that has percolated through a layer of gypsum (\(\ce{CaSO4}\)) with \(K_{sp} = iv.9 \times 10^{–5} = 10^{–4.3}\)) is plant to take exist \(8.4 \times 10^{–five}\; Thousand\) in Ca^{2 +} and \(vii.two \times ten^{–5}\; M\) in So_four ^ii–. What is the equilibrium state of this solution with respect to gypsum?

Solution

The ion production

\[Q_s = (viii.4 \times 10^{–5})(7.2 \times 10^{-5}) = 6.0 \times 10^{–4} \nonumber\]

exceeds \(K_{sp}\), so the ratio \(K_{sp} /Q_{sp} > 1\) and the solution is supersaturated in \(\ce{CaSO_4}\).

Relating Solubilities to Solubility Constants

The solubility (by which nosotros usually mean the molar solubility) of a solid is expressed as the concentration of the "dissolved solid" in a saturated solution. In the case of a simple 1:one solid such as AgCl, this would but be the concentration of Ag⁺ or Cl^– in the saturated solution. Merely for a more complicated stoichiometry such as as silver chromate, the solubility would be but half of the Ag⁺ concentration.

For example, let usa denote the solubility of Ag₂CrO₄ equally Due south mol L^–1. Then for a saturated solution, we have

• \([Ag^+] = 2S\)
• \( [CrO_4^{2–}] = S\)

Substituting this into Eq 5b in a higher place,

\[(2S)^ii (S) = 4S^3 = 2.76 \times 10^{–12}\]

\[S= \left( \dfrac{K_{sp}}{4} \right)^{ane/3} = (6.nine \times 10^{-thirteen})^{1/3} = 0.88 \times 10^{-four} \label{6a}\]

thus the solubility is \(eight.8 \times x^{–5}\; Chiliad\).

Annotation that the relation betwixt the solubility and the solubility product constant depends on the stoichiometry of the dissolution reaction. For this reason it is meaningless to compare the solubilities of two salts having the formulas A₂B and AB₂, say, on the basis of their K_south values.

It is meaningless to compare the solubilities of two salts having different formulas on the basis of their One thousand_s values.

Example \(\PageIndex{2}\)

The solubility of CaF₂ (molar mass 78.ane) at 18°C is reported to be 1.6 mg per 100 mL of water. Summate the value of Chiliad_{due south} under these weather.

Solution

moles of solute in 100 mL; S = 0.0016 g / 78.1 thou/mol = \(2.05 \times ten^{-v}\) mol

\[South = \dfrac{2.05 \times 10^{ –5} mol}{0.100\; 50} = 2.05 \times 10^{-4} M\]

\[K_{sp}= [Ca^{ii+}][F^–]^2 = (Southward)(2S)^2 = 4 × (2.05 \times ten^{–four})^3 = 3.44 \times 10^{–eleven}\]

Example \(\PageIndex{3}\)

Estimate the solubility of La(IO₃)₃ and calculate the concentration of iodate in equilibrium with solid lanthanum iodate, for which K_s = vi.2 × 10^–12.

Solution

The equation for the dissolution is

\[La(IO_3)_3 \rightleftharpoons La^{3+ }+ iii IO_3^–\]

If the solubility is Southward, then the equilibrium concentrations of the ions will be

[La^{3 +}] = South and [IO₃ ^–] = 3Southward. Then K_s = [La³⁺][IO₃ ^–]³ = Southward(3S)³ = 27S ⁴

27S ⁴ = vi.ii × ten^–12, S = ( ( 6.2 ÷ 27) × 10^–12 )^¼ = half-dozen.92 × ten^–four Yard

[IO_iii ^–] = threeS = two.08 × 10^–5 ( M )

Example \(\PageIndex{4}\): Cadmium

Cadmium is a highly toxic environmental pollutant that enters wastewaters associated with zinc smelting (Cd and Zn commonly occur together in ZnS ores) and in some electroplating processes. Ane way of controlling cadmium in effluent streams is to add sodium hydroxide, which precipitates insoluble Cd(OH)_ii (Yard_s = two.5E–14). If 1000 50 of a sure wastewater contains Cd²⁺ at a concentration of 1.6E–5 One thousand , what concentration of Cd²⁺ would remain after add-on of 10 L of four Grand NaOH solution?

Solution

Equally with most real-world problems, this is all-time approached as a series of smaller problems, making simplifying approximations every bit advisable.

Volume of treated water: chiliad Fifty + 10 Fifty = 1010 50

Concentration of OH^– on addition to yard L of pure water:

(iv M ) × (x L)/(1010 L) = 0.040 M

Initial concentration of Cd^{2 +} in 1010 L of water:

\[(ane.6 \times 10^{–5}\; Chiliad) \left( \dfrac{100}{101} \right) \approx 1.6 \times 10^{–5}\; Chiliad\]

The easiest way to tackle this is to start past assuming that a stoichiometric quantity of Cd(OH)_two is formed — that is, all of the Cd^{2 +} gets precipitated.

Concentrations	\([\ce{Cd^{two+}}],\, M\)	\([\ce{OH^{–}}],\, M\)
initial	1.6E–5	0.04
alter	–one.6E–5	–three.2E–5
final:	0	0.04 – 3.2E–v ≈ .04

Now "turn on the equilibrium" — observe the concentration of Cd^{2 +} that can exist in a 0.04 M OH^– solution:

Concentrations	\([\ce{Cd^{two+}}],\, M\)	\([\ce{OH^{–}}],\, G\)
initial	o	0.04
change	+x	+iiten
at equilibrium	ten	.04 + 2x ≈ .04

Substitute these values into the solubility production expression:

Cd(OH)_two (s) = [Cd^{two +}] [OH^–]^two = 2.5E–14

[Cd^{two +}] = (2.5E–fourteen) / (16E–iv) = ane.6E–13 G

Note that the effluent will now be very alkali metal:

\[pH = 14 + \log 0.04 = 12.half-dozen\]
so in order to meet environmental standards an equivalent quantity of strong acid must be added to neutralize the water before information technology is released.

The Common Ion Effect

It has long been known that the solubility of a sparingly soluble ionic substance is markedly decreased in a solution of another ionic compound when the two substances have an ion in common. This is just what would exist expected on the basis of the Le Chatelier Principle; whenever the procedure

\[CaF_{two(s)} \rightleftharpoons Ca^{2+} + 2 F^– \label{vii}\]

is in equilibrium, addition of more fluoride ion (in the form of highly soluble NaF) will shift the composition to the left, reducing the concentration of Ca^{2 +}, and thus effectively reducing the solubility of the solid. Nosotros can express this quantitatively by noting that the solubility production expression

\[[Ca^{2+}][F^–]^ii = i.7 \times x^{–x} \label{8}\]

must always hold, even if some of the ionic species involved come up from sources other than CaF₂ (s) . For example, if some quantity x of fluoride ion is added to a solution initially in equilibrium with solid CaF_two, nosotros have

• \([Ca^{2+}] = Southward\)
• \([F^–] = 2S + x\)

and then that

\[K_{sp} = [Ca^{2+}][ F^–]^2 = Southward (2S + ten)^two . \label{9a}\]

University-level students should exist able to derive these relations for ion-derived solids of whatever stoichiometry. In nearly practical cases x will be large compared to S and so that the iiS term can be dropped and the relation becomes

\[K_{sp} ≈ Southward x^2 \]

\[S = \dfrac{K_{sp}}{x^2} \label{9b}\]

The plots shown below illustrate the common ion event for silver chromate equally the chromate ion concentration is increased by addition of a soluble chromate such as Na₂CrO₄.

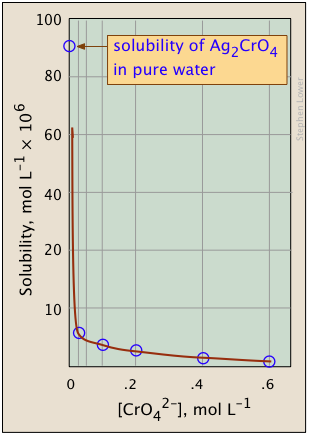
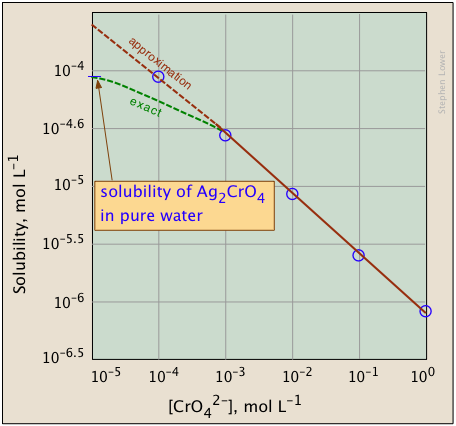
What's different near the plot on the right? If yous expect carefully at the scales, you volition see that this one is plotted logarithmically (that is, in powers of 10.) Discover how a much wider a range of values can display on a logarithmic plot. The signal of showing this pair of plots is to illustrate the keen utility of log-concentration plots in equilibrium calculations in which uncomplicated approximations (such as that made in Equation \(\ref{9b}\)) can yield straight-lines within the range of values for which the approximation is valid.

Example \(\PageIndex{5}\): strontium sulfate

Calculate the solubility of strontium sulfate (Thou_s = 2.8 × x^–seven) in

1. pure h2o and
2. in a 0.10 mol Fifty^–1 solution of Na₂SO_iv.

Solution:

(a) In pure water, Chiliad_s = [Sr^{2 +}][SO₄ ^2–] = S ²

S = √One thousand_s = (2.8 × x^–7)^½ = 5.3 × 10^–4

(b) In 0.10 mol 50^–1 Na₂And then₄, we accept

K_s = [Sr^{2 +}][And then₄ ^two–] = S × (0.10 + S) = two.8 × x^–7

Considering Due south is negligible compared to 0.x Chiliad, we brand the approximation

K_southward = [Sr^{2 +}][Then₄ ^2–] ≈ S × (0.10 M) = two.8 × 10^–vii

so S ≈ (ii.eight × x^–7) / 0.10M = 2.viii × 10^–6 M — which is roughly 100 times smaller than the result from (a).

Notation

The common ion result normally decreases the solubility of a sparingly soluble table salt.

Example \(\PageIndex{half-dozen}\)

Calculate the solubility of calcium phosphate [Ca₃(PO₄)_two] in 0.xx One thousand CaCl₂.

Given: concentration of CaCl₂ solution

Asked for: solubility of Ca₃(PO₄)₂ in CaCl₂ solution

Strategy:

1. Write the balanced equilibrium equation for the dissolution of Ca_three(PO₄)₂. Tabulate the concentrations of all species produced in solution.
2. Substitute the appropriate values into the expression for the solubility product and calculate the solubility of Ca₃(PO₄)₂.

Solution

A The balanced equilibrium equation is given in the following table. If we let 10 equal the solubility of Ca₃(PO₄)₂ in moles per liter, and then the change in [Ca^{two +}] is once again +threex, and the change in [PO₄ ³⁻] is +2x. Nosotros can insert these values into the ICE table.

\[Ca_3(PO_4)_{2(s)} \rightleftharpoons 3Ca^{two+} (aq) + 2PO^{3−}_{4(aq)}\]

	\(\ce{Ca3(PO4)ii}\)	\(\ce{[Ca2+]}\)	\(\ce{[PO43−]}\)
initial	pure solid	0.20	0
change	—	+3ten	+iiten
final	pure solid	0.twenty + 310	twoten

B The K _sp expression is equally follows:

Yard _sp = [Ca^{2 +}]^three[PO_iv ^three−]² = (0.20 + 3x)³(2ten)² = ii.07×10⁻³³

Because Ca₃(PO_iv)_two is a sparingly soluble salt, nosotros can reasonably expect that x << 0.20. Thus (0.20 + threex) G is approximately 0.twenty G, which simplifies the K _sp expression as follows:

\[\begin{align}K_{\textrm{sp}}=(0.20)^three(2x)^2&=ii.07\times10^{-33}
\\x^2&=6.5\times10^{-32}
\\x&=two.5\times10^{-sixteen}\textrm{ Yard}\end{marshal}\]

This value is the solubility of Ca_three(PO_four)₂ in 0.xx M CaCl₂ at 25°C. It is approximately nine orders of magnitude less than its solubility in pure water, as we would expect based on Le Chatelier's principle. With i exception, this example is identical to Example \(\PageIndex{2}\)—here the initial [Ca^{two +}] was 0.twenty Grand rather than 0.

Exercise \(\PageIndex{vi}\)

Calculate the solubility of silver carbonate in a 0.25 M solution of sodium carbonate. The solubility of silver carbonate in pure water is 8.45 × 10⁻¹² at 25°C.

Answer

2.9 × x⁻⁶ M (versus 1.3 × x⁻⁴ 1000 in pure water)

Applications and Examples

Precipitation reactions are useful in determining whether a sure element is nowadays in a solution. If a precipitate is formed when a chemic reacts with lead, for instance, the presence of lead in h2o sources could be tested by adding the chemical and monitoring for precipitate formation. In addition, precipitation reactions can exist used to extract elements, such as magnesium from seawater. Atmospheric precipitation reactions even occur in the human body betwixt antibodies and antigens; all the same, the environment in which this occurs is nonetheless being studied.

Instance \(\PageIndex{seven}\)

Consummate the double replacement reaction and then reduce it to the internet ionic equation.

\[NaOH (aq) + MgCl_{ii \;(aq)} \rightarrow \nonumber \]

Commencement, predict the products of this reaction using knowledge of double replacement reactions (recall the cations and anions "switch partners").

\[2NaOH (aq) + MgCl_{2\;(aq)} \rightarrow 2NaCl + Mg(OH)_2 \nonumber\]

Second, consult the solubility rules to decide if the products are soluble. Grouping ane cations (\(Na^+\)) and chlorides are soluble from rules one and three respectively, so \(NaCl\) volition be soluble in water. Withal, rule 6 states that hydroxides are insoluble, and thus \(Mg(OH)_2\) will form a precipitate. The resulting equation is the following:

\[2NaOH(aq) + MgCl_{2\;(aq)} \rightarrow 2NaCl (aq) + Mg(OH)_{2\;(s)} \nonumber\]

Third, separate the reactants into their ionic forms, equally they would exist in an aqueous solution. Exist certain to remainder both the electrical accuse and the number of atoms:

\[2Na^+ (aq) + 2OH^- (aq) + Mg^{2+} (aq) + 2Cl^- (aq) \rightarrow Mg(OH)_{ii\;(s)} + 2Na^+ (aq) + 2Cl^- (aq) \nonumber\]

Lastly, eliminate the spectator ions (the ions that occur on both sides of the equation unchanged). In this case, they are the sodium and chlorine ions. The final net ionic equation is:

\[Mg^{two+} (aq) + 2OH^- (aq) \rightarrow Mg(OH)_{2(s)} \nonumber\]

Case \(\PageIndex{eight}\)

Consummate the double replacement reaction and and then reduce information technology to the net ionic equation.

\[CoCl_{two\;(aq)} + Na_2SO_{4\;(aq)} \rightarrow \nonumber\]

Solution

The predicted products of this reaction are \(CoSO_4\) and \(NaCl\). From the solubility rules, \(CoSO_4\) is soluble because rule 4 states that sulfates (\(SO_4^{2-}\)) are soluble. Similarly, we detect that \(NaCl\) is soluble based on rules ane and three. Subsequently balancing, the resulting equation is as follows:

\[CoCl_{2\;(aq)} + Na_2SO_{iv\;(aq)} \rightarrow CoSO_{4\;(aq)} + 2 NaCl (aq) \nonumber\]

Separate the species into their ionic forms, as they would exist in an aqueous solution. Residuum the charge and the atoms. Abolish out all spectator ions (those that appear as ions on both sides of the equation.):

Co ^{2 -} (aq) + 2Cl ^-(aq) + 2Na ⁺ (aq) + SO_four ^{ii -}(aq) → Co ^{2 -} (aq) + Then_iv ^{2 -}(aq) + 2Na ⁺ (aq) + 2Cl ^-(aq)

No precipitation reaction

This particular example is important because all of the reactants and the products are aqueous, pregnant they cancel out of the net ionic equation. There is no solid precipitate formed; therefore, no precipitation reaction occurs.

Example \(\PageIndex{9}\)

Write the net ionic equation for the potentially double displacement reactions. Make sure to include the states of affair and residue the equations.

1. \(Iron(NO_3)_{3\;(aq)} + NaOH (aq) \rightarrow\)
2. \(Al_2(SO_4)_{3\;(aq)} + BaCl_{ii\;(aq)} \rightarrow\)
3. \(HI (aq) + Zn(NO_3)_{two\;(aq)} \rightarrow\)
4. \(CaCl_{2\;(aq)} + Na_3PO_{4\;(aq)} \rightarrow\)
5. \(Pb(NO_3)_{2\;(aq)} + K_2SO_{four \;(aq)} \rightarrow\)

Solutions

a. Regardless of physical state, the products of this reaction are \(Fe(OH)_3\) and \(NaNO_3\). The solubility rules predict that \(NaNO_3\) is soluble considering all nitrates are soluble (rule 2). Nevertheless, \(Fe(OH)_3\) is insoluble, considering hydroxides are insoluble (rule 6) and \(Atomic number 26\) is not one of the cations which results in an exception. Afterward dissociation, the ionic equation is as follows:

\[Atomic number 26^{3+} (aq) + NO^-_{3\;(aq)} + Na^+ (aq) + 3OH^- (aq) \rightarrow Atomic number 26(OH)_{three\;(s)} + Na^+ (aq) + NO^-_{3\;(aq)} \nonumber\]

Canceling out spectator ions leaves the cyberspace ionic equation:

\[Fe^{3+} (aq) + OH^- (aq) \rightarrow Fe(OH)_{\;3(s)} \nonumber\]

b. From the double replacement reaction, the products are \(AlCl_3\) and \(BaSO_4\). \(AlCl_3\) is soluble because it contains a chloride (rule three); nonetheless, \(BaSO_4\) is insoluble: it contains a sulfate, but the \(Ba^{two+}\) ion causes it to exist insoluble because it is i of the cations that causes an exception to rule four. The ionic equation is (after balancing):

\[2Al^{iii+} (aq) + 6Cl^- (aq) + 3Ba^{2+} (aq) + 3SO^{2-}_{4\;(aq)} \rightarrow 2 Al^{3+} (aq) +6Cl^- (aq) + 3BaSO_{four\;(southward)} \nonumber\]

Canceling out spectator ions leaves the following net ionic equation:

\[Ba^{2+} (aq) + And then^{2-}_{four\;(aq)} \rightarrow BaSO_{4\;(south)} \nonumber\]

c. From the double replacement reaction, the products \(HNO_3\) and \(ZnI_2\) are formed. Looking at the solubility rules, \(HNO_3\) is soluble considering it contains nitrate (rule ii), and \(ZnI_2\) is soluble because iodides are soluble (dominion iii). This means that both the products are aqueous (i.e. dissociate in water), and thus no precipitation reaction occurs.

d. The products of this double replacement reaction are \(Ca_3(PO_4)_2\) and \(NaCl\). Rule 1 states that \(NaCl\) is soluble, and according to solubility rule half dozen, \(Ca_3(PO_4)_2\) is insoluble. The ionic equation is:

\[Ca^{two+} (aq) + Cl^- (aq) + Na^+ (aq) + PO^{3-}_{iv\;(aq)} \rightarrow Ca_3(PO_4)_{2\;(s)} + Na^+ (aq) + Cl^- (aq) \nonumber \]

After canceling out spectator ions, the net ionic equation is given below:

\[Ca^{2+} (aq) + PO^{3-}_{4\;(aq)} \rightarrow Ca_3(PO_4)_{2\;(s)} \nonumber\]

e. The kickoff production of this reaction, \(PbSO_4\), is soluble according to rule 4 because it is a sulfate. The second production, \(KNO_3\), is as well soluble because information technology contains nitrate (dominion two). Therefore, no precipitation reaction occurs.

References

1. Campbell, Dan, Linus Pauling, and Davis Pressman. "The Nature of the Forces Betwixt Antigen and Antibody and of the Atmospheric precipitation Reaction." Physiological Reviews 23.3 (1943): 203-219. Online.
2. Harwood, William, F Herring, Jeffry Madura, and Ralph Petrucci. Full general Chemistry. 9th ed. Upper Saddle River: Pearson Pretence Hall, 2007. Print.
3. Freeouf, J.L, Grischkowsky, D., McInturff, D.T., Warren, A.C., & Woodall, J.M. (1990). Arsenic precipitates and the semi-insulating properties of gaas buffer layers grown by depression-temperature molecular beam epitaxy. Practical Physics Letters, 57(thirteen)
4. Petrucci, et al. General Chemical science: Principles & Modern Applications. ninth ed. Upper Saddle River, New Jersey 2007.

Summary

In contrast to \(K_{sp}\), the ion product (\(Q_{sp}\)) describes concentrations that are not necessarily equilibrium concentrations. Comparing Q and Thou _sp enables united states to decide whether a precipitate will form when solutions of ii soluble salts are mixed. Adding a common cation or common anion to a solution of a sparingly soluble salt shifts the solubility equilibrium in the direction predicted by Le Chatelier'due south principle. The solubility of the table salt is almost always decreased past the presence of a common ion.

Source: https://chem.libretexts.org/Bookshelves/General_Chemistry/Map%3A_Principles_of_Modern_Chemistry_(Oxtoby_et_al.)/Unit_4%3A_Equilibrium_in_Chemical_Reactions/16%3A_Solubility_and_Precipitation_Equilibria/16.3%3A_Precipitation_and_the_Solubility_Product

Share this post